Suggested Answers to 2015 A Level H2 Math 9740 PAPER 2

 

1. Differential equation

(i) h = 32m

(ii) ≈ 46.9 years

 

2. Vectors

(i) ≈ 73.4°

(ii) λ = 3/7 or 1

Point = ( 17/7 , 1/7 , -58/7 )

(iii) -36x + 2y – 11z = 4

 

3. Functions

a)(i) Graph of y=k , k∈R , cuts at most on 1 point.

f (x) is a 1 – 1 function, f inverse exists

(ii) f -¹ : x → √(1 – 1/x) , x > 0

b) y≤ 1 – (1/2)√3  or  y≥ 1 + (1/2)√3

Rg = ( -∞, 1 – (1/2)√3] ∪ [ 1 + (1/2)√3 , ∞ )

 

4. Mathematical induction / Method of difference

b)(i) 2 = A(2r+3) + B(2r+1)

(ii) (1/3) – (1/(2n+3))

(iii) n≥ 1498.5

smallest n = 1499

 

5. Sampling methods

(i)  Sampling frame is not available, therefore the manager is unable to define the appropriate subgroups required for stratified sampling.

(ii)  Survey 25 people each for different age groups  (5-20, 21-40, 41-60, 61-80). The manager can survey the customers going in and out of the supermarket to obtain the  required data.

6. Binomial distribution

(i) ≈ 0224

(ii) ≈ 0.149

(iii) ≈ 0.825

 

7. Poisson distribution

(i) Average number of errors per page is constant

Errors occurring are independent of each other

(ii) ≈ 0.165

(iii) least n = 4

 

8. Hypothesis Testing

p-value = 0.264618 > 0.1

Do not reject Ho. There is insufficient evidence at the 10% level of significance to doubt his claim.

 

9. Probability

(i) = 0.4

(ii) 0.185

(iii) Lowest = 0.165

Highest = 0.33

 

10. Correlation and Regression 

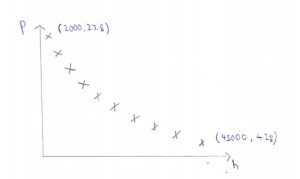
i)

(ii) a. ≈ -0.9807

b. ≈ -0.9748

c. ≈ -0.9986

(iii) √h and P

P = 34.8 – 0.266√h

(iv) 34.8 – 0.266√h

 

11. Permutations and Combinations

(i) 10080

(ii) 10079

(iii) 720

(iv) 5760

 

12. Normal Distribution

(i) 0.01267

(ii) 0.05238

(iii) 0.742

 

 

 

 

A-LEVEL H2 MATH JUNE HOLIDAYS INTENSIVE REVISION

A-LEVEL H2 PHYSICS JUNE HOLIDAYS INTENSIVE REVISION

 

JUNIOR COLLEGE / A-LEVEL TUITION: