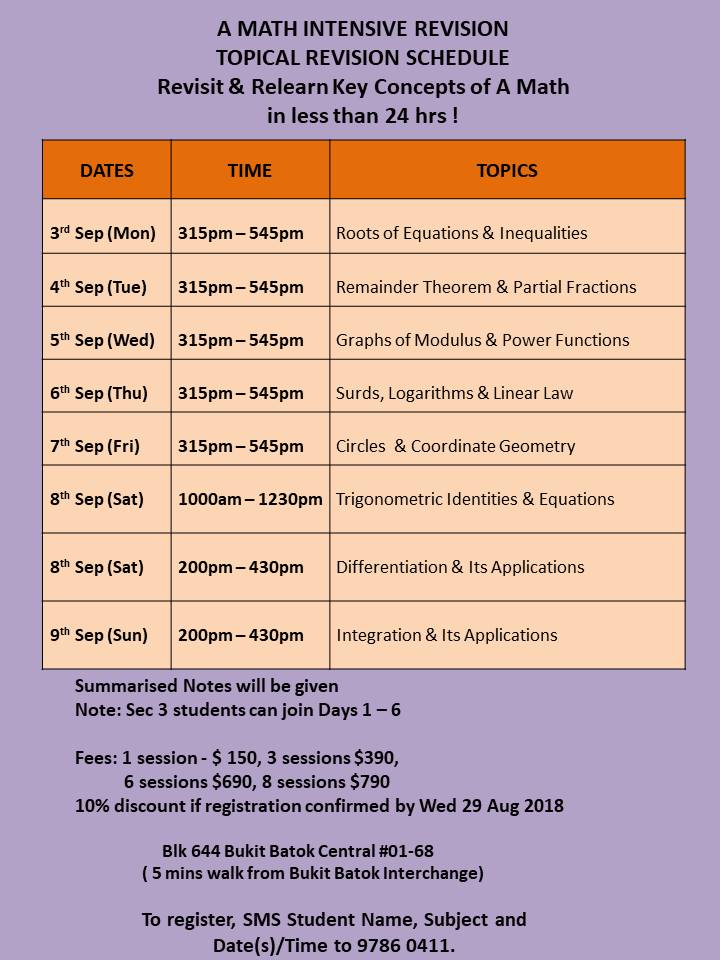
Revisit & Relearn Key Concepts of A Math in less than 24 hrs!
Our experienced tutor is prepared to go through specific topics of A Math to aid in your exam preparation.
He is an NIE trained ex MOE school teacher who has been COACHING students to master A. Math for more than 12 years.
SCHEDULE
Days: 3rd Sep – 7th Sep (Mon – Fri)
Time: 315 pm – 545 pm
8th Sep (Sat)
Time: 10 am – 1230 pm
8th Sep – 9th Sep
Time: 2 pm – 4.30 pm
Location: Blk 644, Bukit Batok Central, #01-68. S(650644).
Target Group: Current Sec 3/4 students who cannot seem to reach their intended grades despite great effort.
(Sec 3 students can attend Day 1 – Day 6)
To sign up, SMS <Student name>, <SepAMath>,<Date>,<Time> to +(65) 9786 0411.
Sec 4 A. Math Reflections 02/02/13 – Higher Derivative
Today I taught them the Higher Derivatives, using displacement, velocity and acceleration as real-life examples. I chose not to introduce the 2nd derivative as a means to test whether a turning point is a maximum or minimum, as I preferred to do that when teaching the application of differentiation in tangents and normals at a point in a curve.
Points to note:
(1) students must not write the 2nd derivative as dy^2/dx^2;
(2) d^2y/dx^2 is not the same as (dy/dx)^2;
(3) d^2y/dx^2 is the same as f”(x) or f^2(x);
(4) there may be product rule, quotient rule or chain rule involved when finding the higher derivatives.
Rgds,
Ilyasa, M.Ed, PGDE, ex-MOE Math and Physics teacher (hp: 97860411)
_______________________________________
TUITION CLASSES:
_______________________________________________________________
EDUCATIONAL SERVICES:
______________________________________________________________
By EX-MOE TEACHERS & EXPERIENCED TUTORS
@ BLK 644, BUKIT BATOK CENTRAL, #01-68. S(650644).
CALL 65694897 OR SMS 98530744 OR 97860411.
Sec 4 A. Math Reflections sat1415 19/01/2013 – Differentiation
This was our third lesson in Jan. We did the Product Rule for Differentiation after spending the last two sessions doing the Basic Rule and the Power Rule (a subset of the chain rule).
I told students to differentiate directly, in line, and not use the “let u = f(x) and v = g(x)” which is longer, more confusing and can cause more careless mistakes.
Now they are able to perform dy/dx = f(x)g'(x) + g(x)f'(x) quite quickly without introducing new variables such u and v which can be quite clumsy. Most of the time, finding dy/dx is part of a larger question, so it is unwise to make this part too long.
I ended the lesson with an intro to the Quotient Rule. Again, I don’t recommend the use of u’s and v’s and instead differentiate directly in line. We’ll be practising the Quotient Rule in the next session.
Again I tell students that Calculus is almost one-third of the A. Math syllabus, so if you want to get A1 you have to master Differentiation and Integration, which, in my opinion (and students hate it every time I say it), are amongst the easiest of topics in A.Math.
However, Integration at the A-Levels (H2 Math) can be quite difficult. But we’ll cross the bridge when we come to it. : )
Ilyasa, M.Ed, PGDE, ex-MOE teacher
(hp: 97860411)
=============================================================
For our latest timetable, click here => 
=============================================================
Is metacognition part of the mathematics curriculum in Singapore?
One of the aims of mathematics education in schools in Singapore is to enable students to acquire thinking and problem solving skills and to make effective use of these skills to formulate and solve problems (MOE, 2007).
The existing curriculum framework for mathematics designed by the Ministry of Education (MOE) lists metacognition as one of the components on which the development of mathematical problem solving ability depends.
According to the MOE (2007), metacognition can be defined as the realization of, and the ability to regulate one’s thinking processes, in particular the choosing and application of problem-solving strategies. The MOE believes that it is important to provide students with metacognitive experience in order to help them develop their problem solving abilities.
Note: The above paragraphs are adapted from my minor research paper, Examining Supports for Metacognition in Singaporean Lower Secondary Mathematics Textbooks, NIE, 2011. All rights reserved.
Related links:
(1) Metacognition – The secret to learning and problem-solving;
(2) Metacognition and problem-solving;
(3) Metacognition enhances learning;
_______________________________________
TUITION CLASSES:
_______________________________________________________________
EDUCATIONAL SERVICES:
______________________________________________________________
By EX-MOE TEACHERS & EXPERIENCED TUTORS
@ BLK 644, BUKIT BATOK CENTRAL, #01-68. S(650644).
CALL 65694897 OR SMS 98530744 OR 97860411.
Metacognition and mathematical problem solving
Metacognition is a crucial element in problem-solving, which is itself a key component in mathematics learning. To monitor and regulate one’s cognitive processes in problem-solving, Polya (1945) describes a four-step method: first, one has to comprehend the problem by sub-dividing it into more manageable parts and recognize any given data, conditions and variables to be found; second, one devises or selects a strategy to find the connections between the known data and the unknowns to be found; third, one executes the plan, scanning, regulating and examining each step; and, finally, after obtaining the solution, one evaluates the results which may involve re-visiting the previously taken steps.
Building on Polya’s work, Schoenfeld (1987) describes effective mathematical problem-solving as being contingent on how one uses four types of knowledge/skills: (1) resource knowledge, which is knowledge about one’s abilities and cognitive processes including knowledge of how to perform tasks or procedures; (2) heuristics, which are specific problem-solving methods or strategies; (3) regulatory processes, which includes the organisation and selection of resources and strategies; and (4) beliefs, which includes perceptions of and assumptions about mathematics (Gama, 2004).
Note: The above paragraphs are adapted from my minor research paper, Examining Supports for Metacognition in Singaporean Lower Secondary Mathematics Textbooks, NIE, 2011. All rights reserved.
Related links:
(1) Metacognition – The secret to learning and problem-solving;
(2) Metacognition enhances learning;
(3) Is Metacognition part of the Singapore Math curriculum?
_______________________________________
TUITION CLASSES:
_______________________________________________________________
EDUCATIONAL SERVICES:
______________________________________________________________
By EX-MOE TEACHERS & EXPERIENCED TUTORS
@ BLK 644, BUKIT BATOK CENTRAL, #01-68. S(650644).
CALL 65694897 OR SMS 98530744 OR 97860411.
A. Math Reflections & Study Tips
(1) Simultaneous Equations
Generally an easy topic, but beware of certain kinds of questions such as:
(a) Questions involving reciprocals of x and y, such as
Solve 3(1/x) + 1/y = 1; 1/(x^2) + 1/(y^2) = 5
Ans: x = 1, y = -1/2 or x = -5/2, y = 5/11
Do not make common denominators and cross-multiply; the better technique is to let p = 1/x and q = 1/y.
(b) Questions involving coefficient matrices that are singular (determinant = 0), such as
Given that x and y satisfy the simultaneous equations mx + (m-1)y = 10 and (m-2)x + 3my = 20,
(i) if the equations have no unique solution, find the values of m; (ans: 1/2, -2)
(ii) if the equations have no solution, find the value of m.(ans: 1/2)
(adapted from Additional Math, EPB Panpac, p. 13)
(2) Indices, Surds & Logarithms
Generally an easy topic, except for students who do not understand or memorize the laws of indices and logarithms properly. I find that quite a number of weak students do not know the meaning of logarithm, thus not appreciating and enjoying the topic. Weak students do not realize that while Indices is concerned with the answer or expression obtained when a power is applied to a base number, Logarithms is about the power itself; the power that is needed to be applied to a base to give a certain number.
For eg, why is lg1000 = 3? ‘Evaluate lg1000’ or ‘What is lg1000?’ is the same as asking, “What is the Power that must be applied to the number 10 (the base) to obtain 1000?” Since 10^3 = 1000, therefore the answer is 3.
Weak students almost always make one or more of the following mistakes, thinking that (i) logA x logB = logA + logB, (ii) log(A + B) = logA + logB, (iii) logAB = logA x logB, (iv) (logA)^n = nlogA, (v) logAB^n = nlogAB, (vi) (a^m)^n = a^(m+n). All these are wrong.
How to be good in Indices and Logarithms? READ AND UNDERSTAND THE LAWS OF INDICES AND LOGARITHMS CAREFULLY. Yes, there is such a thing as READING MATH, not just practising Math.
(3) Quadratic Functions & Equations
Some of the points to note are:
(1) Understand that alpha and beta by themselves also satisfy the quadratic eqn because they are the roots of the equation! So it’s not just abt finding the sum and product of roots;
You must be able to solve questions like:
If α is the root of the equation x^2 = 2x – 1, show that α^4 – α^2 = 2α – 2.
(2) Understand that the discriminant (b^2 – 4ac) is less than or equal to zero when the question involves the phrase “for which the function is never positive or never negative”;
(3) Understand that sometimes you are required to solve an inequality involving the discriminant but at other times the inequality involves the function itself;
(4) Understand how to complete the square to determine the maximum or minimum value of a quadratic function;
(5) Recognise that “real and distinct roots”, “real and equal roots”, and “no real roots” have other names that express the same meaning.
TO BE CONTINUED ……….. (by Mr Ilyasa)
===================================================
For our latest timetable, click here =>