1. Differential equation
(i) h = 32m
(ii) ≈ 46.9 years
2. Vectors
(i) ≈ 73.4°
(ii) λ = 3/7 or 1
Point = ( 17/7 , 1/7 , -58/7 )
(iii) -36x + 2y – 11z = 4
3. Functions
a)(i) Graph of y=k , k∈R , cuts at most on 1 point.
f (x) is a 1 – 1 function, f inverse exists
(ii) f -¹ : x → √(1 – 1/x) , x > 0
b) y≤ 1 – (1/2)√3 or y≥ 1 + (1/2)√3
Rg = ( -∞, 1 – (1/2)√3] ∪ [ 1 + (1/2)√3 , ∞ )
4. Mathematical induction / Method of difference
b)(i) 2 = A(2r+3) + B(2r+1)
(ii) (1/3) – (1/(2n+3))
(iii) n≥ 1498.5
smallest n = 1499
5. Sampling methods
(i) Sampling frame is not available, therefore the manager is unable to define the appropriate subgroups required for stratified sampling.
(ii) Survey 25 people each for different age groups (5-20, 21-40, 41-60, 61-80). The manager can survey the customers going in and out of the supermarket to obtain the required data.
6. Binomial distribution
(i) ≈ 0224
(ii) ≈ 0.149
(iii) ≈ 0.825
7. Poisson distribution
(i) Average number of errors per page is constant
Errors occurring are independent of each other
(ii) ≈ 0.165
(iii) least n = 4
8. Hypothesis Testing
p-value = 0.264618 > 0.1
Do not reject Ho. There is insufficient evidence at the 10% level of significance to doubt his claim.
9. Probability
(i) = 0.4
(ii) 0.185
(iii) Lowest = 0.165
Highest = 0.33
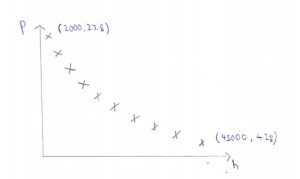
10. Correlation and Regression
i)
(ii) a. ≈ -0.9807
b. ≈ -0.9748
c. ≈ -0.9986
(iii) √h and P
P = 34.8 – 0.266√h
(iv) 34.8 – 0.266√h
11. Permutations and Combinations
(i) 10080
(ii) 10079
(iii) 720
(iv) 5760
12. Normal Distribution
(i) 0.01267
(ii) 0.05238
(iii) 0.742
A-LEVEL H2 MATH JUNE HOLIDAYS INTENSIVE REVISION
A-LEVEL H2 PHYSICS JUNE HOLIDAYS INTENSIVE REVISION
JUNIOR COLLEGE / A-LEVEL TUITION:
_______________________________________________________________________
______________________________________________________________
By EX-MOE TEACHERS & EXPERIENCED TUTORS
@ BLK 644, BUKIT BATOK CENTRAL, #01-68. S(650644).
CALL 65694897 OR SMS 98530744 OR 97860411.
Suggested Answers to 2015 A Level H2 Math 9740 PAPER 1
1. System of linear equations / Graphing techniques
(i) a = -3.953 , b = -5.187 , c = 7.303
(ii) x = -0.589
(iii) y = 5.19x + 7.3
2. Graphing techniques / Inequalities
i)
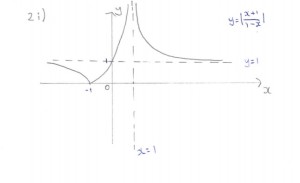
(ii) -1.73 < x < 0.414 or x > 1.73
3. Integration
(i) When n→∞ , sum of area of rectangles ≈ area of function
(ii) 3/4
4. Application of differentiation
Maximum area = (1/32) d²
5. Graphing techniques / Transformation
(i) Translation of +3 units parallel to the x-axis,
Scaling by scale factor of 1/4 parallel to the y-axis
ii)
iii)
6. Maclaurin’s series / Binomial expansion
(i) 2x – 2x² + (8x³/3)
(ii) -(104/27)
7. Vectors
(i) OC = (3/5)a
OD = (5/11)b
(ii) line BC : r = (3/5)λa + (1 – λ)b
line AD : r = (1 – μ)a + (5/11)μb
(iii) AE : ED = 11:9
8. AP/GP
(i) T = { T∈R : 59 ≤ T ≤ 77 }
(ii) t = { t∈R : 63.8 ≤ t ≤ 74.5 }
9. Complex numbers
a) w = a ± (a/√3)i
b)(i) z = 2e^(-π/10) , 2e^(3π/10) , 2e^(-π/2) , 2e^(7π/10) , 2e^(-9π/10)
(ii) 4 sin ( π/5)
10. Application of integration
i) A1/A2 = (2-√2)/(√2 -1)
= √2
iii) Volume = (π³/16√2) + (π²/2√2) – √2 π
11. Application of differentiation and integration
i) dy/dx = (-3sin³Θ + 6sinΘ cos²Θ)/(3sin²Θ cosΘ)
= 2 cot Θ – tan Θ (shown)
ii) ( (2√2)/(3√3) , ( 2 /√3 ) ) maximum point
iii) Area ≈ 0.884
iv) a = (3√2)/(2)
A-LEVEL H2 MATH JUNE HOLIDAYS INTENSIVE REVISION
A-LEVEL H2 PHYSICS JUNE HOLIDAYS INTENSIVE REVISION
JUNIOR COLLEGE / A-LEVEL TUITION:
_______________________________________________________________________
______________________________________________________________
By EX-MOE TEACHERS & EXPERIENCED TUTORS
@ BLK 644, BUKIT BATOK CENTRAL, #01-68. S(650644).
CALL 65694897 OR SMS 98530744 OR 97860411.
Suggested Answers to 2014 A Level H2 Math 9740 PAPER 2
NEW!
H2 PHYSICS PRACTICAL
H2 CHEMISTRY PRACTICAL
H2 BIOLOGY PRACTICAL
The following is a suggested solution by our H2 and H1 Math Tutor, Mr. Teng. Please note that it is a suggested solutions and was rushed out. Mr. Teng omitted several presentation steps out of convenience. There might be alternative solutions at times too. Feel free to comment and discuss. Please let us know if there are mistakes too. Thanks in advance.
PLEASE NOTE THAT STUDENTS ARE EXPECTED TO WRITE STATE YOUR DISTRIBUTIONS CLEARLY. We omitted for convenience.
Disclaimer: This suggested solutions is provided free by Mr. Teng & Singapore Learner. Both parties do not profit from this. We simply believe that this will help current students and future students to learn from the mistakes of others. Thanks.
ERRATA & Remarks:
6(ii) I miscounted and was careless.
Case 1: A plays midfield, B sits out of attacker =>3c1 x 8c4 x 4c1 x 5c4
Case 2: A sits out midfield, B plays attacker => 3c1 x 8c4 x 4c2 x 5c3
Case 1 + Case 2 =1 6800
(iii) I doubled counted indeed. Thanks for pointing out. Should be
Case 1: Midfielder A plays midfield => 8c4 x 3c1
Case 2: Midfielder A plays defender => 8c3 x 3c2
Case 3: Midfielder A sits out => 8c4 x 3c2
3c1 x 5c4 x (8c4 x 3c1 + 8c3 x 3c2 + 8c4 x 3c2) = 8820
8ai. I drew the left side of the quadratic. It should be the right side. my bad.
9. I initially used Z-Test for this question. But T-test is definitely more appropriate as we are given as unknown population variance. I changed it to T-test in the following solutions, but understand that some teachers consider Z-Test to be acceptable too. I should highlight that nobody has access to the actual answer scheme; we only see the marker’s report.
(ii), (iii) Set notations should be used. {t>3.48} and {0<k^2<0.423}
11. Please take note that I used CLT here, so cc is not required.
– I understand some students misunderstand that CLT is used to find the mean of any distribution. This is a terrible misconception. CLT is a limiting theorem, and we apply it to approximate a non-normal distribution to a normal distribution, given n is sufficient. And they can be sum of independent random variables, sample sum, or sample mean. You can read more from the link below.
– Why I used CLT approximation instead of poisson approximation (Poisson approximation is not incorrect either): I used continuity correction in qn 7 alr, so given examiner psychology, I would think they want to be impressed with something different. That’s why I picked CLT approximation. Do note that this does not mean that doing poisson approximation is wrong; so long as you perform cc precisely.
I do hope this clarifies, and I’m sorry it came late as I was ill and had jc1 classes yesterday too.
_______________________________________
TUITION CLASSES:
_______________________________________________________________
EDUCATIONAL SERVICES:
______________________________________________________________