For our latest timetable, click here => 
===============================================================
ORIGINAL POST(OUTDATED):
For enquires, pls call 97860411, or visit www.conceptlearning.sg
To register for classes at Concept Learning, click here.
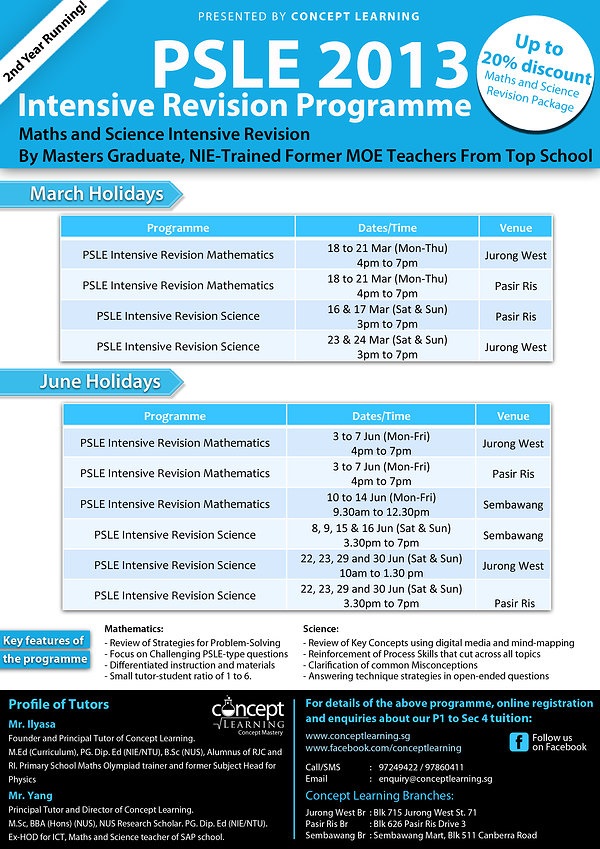
The PSLE Intensive Revision in Mathematics is a 4/5-day intensive revision programme conducted during the upcoming March and June school holidays to prepare P6 pupils for the 2013 PSLE Mathematics Examination.
The objectives of the programme are as follows:
- Review of problem-solving strategies to conquer Challenging PSLE maths problems using the Conceptual Approach such as Advance Model Drawing, Remainder Concept (Branching), Repeated Identity, Equal Concept, Unchanged Total, Proportions Concept and Constant Difference. The strategies cuts across the major topics in PSLE such as fractions, ratio, percentage, decimals, measurement and numbers.
- Review and the reinforcement of key topics such as Percentage, Ratio, Fractions, Decimals, Algebra, Geometry, Area and Perimeter and Volume.
A former MOE school teacher, Mr Ilyasa has been coaching students in ‘A’ Level (H2/H1) Physics and (H2/H1) Mathematics for more than 7 years, as well as ‘O’ Level Physics, Additional Math, Math and PSLE Math for more than 10 years. An alumnus of RI and RJC, Mr Ilyasa holds a Bachelor of Science degree with Merit from the National University of Singapore, a Postgraduate Diploma in Education with Credit from the National Institute of Education, Singapore, and a Master of Education (Curriculum & Teaching) degree also from the NIE, Singapore.
Reflections on PSLE Math Intensive Revision recently held at Concept Learning
I’ve been wanting to write abt this for some time. For the four days of the PSLE Math Intensive Revision we covered topics such as Remainder Concept, Constant Difference Concept, Internal Transfer Concept and so on, with each worksheet having questions of increasing difficulty involving whole numbers, decimals, fractions, ratios and percentages. For most of the questions, I showed more than one method of solving them, for eg., by using model drawings, units, or the branch method and so on.
So what did I discover from conducting the course? I’m surprised to learn from the students that schools do not cover all the methods I demonstrated, maybe due to a lack of time. And the students, who were abt medium to high ability in math, could solve difficult questions if the question involves only one concept or one method. If the question involves fractions, ratios, decimals and percentages all at the same time, or the question is best done using the branch method first followed by models drawing, then many of the students could not completely solve the problem.
How to overcome the above problem? Students need to understand that fractions, ratios, decimals and percentages all just different forms of the same proportion of quantities, and are thus easily convertible from one form to the other. But students must first understand each concept properly first; for example, what does it mean if the problem has the phrase “John has 25% percent more marbles than Alvin”? If a student is comfortable with using the ratio method to solve problems, but is unable to rewrite the above phrase in ratio form, then he may not be able to proceed with solving the rest of the problem.
Some questions involve more than one concept. For example, it contains a phrase such as “Alvin sold some marbles and gave 40% of the remainder to Susan and Eugene, with Susan getting 20 more marbles than Eugene.” A well-trained student would be able to use a number of methods to solve a difficult problem.
I’m also surprised that some students do not know how to check whether their answers are correct. Since most tough questions require students to work backwards to find some unknown starting quantity, then the student can verify the correctness of his answer by working “forward” with the now known starting quantity and try to obtain all the other quantities given in the question.
The key to solving PSLE math problems is to understand that either a quantity has remained unchanged, or is equal to another, or can be made equal to another. Then the different methods (models, units, branch etc) can be applied.
A very bright student once said to me – “Whether you draw models or use units or use algebra is not important. You must first understand the nature of the problem.”
Good luck.
Ilyasa.
Mr Ilyasa is the Principal Tutor at Concept Learning and Singapore Learner. He can be contacted at 97860411, or ilyasa@conceptlearning.sg.
* If you are medium or high ability student preparing for PSLE Math, you may want to attend my weekly workshop: Challenging PSLE Math Programme for Medium to High Ability Students. In this programme, I will also include P6 Math Olympiad problems that are relevant to the PSLE.
_______________________________________
TUITION CLASSES:
_______________________________________________________________
EDUCATIONAL SERVICES:
______________________________________________________________








