Dates: Friday 2/10 and 9/10.
Time: 4.00 pm – 6.30 pm
Location: Blk 644, Bukit Batok Central, #01-68. S(650644).
Target Group & Purpose: P4 students who wish to REVISE or LEARN various efficient methods to solve challenging word problems FAST and CORRECTLY, such as the Bar Model method, Units Method, Branch Method, Sets method, Conversion method etc.
Topics covered: WHOLE NUMBERS, FRACTIONS, DECIMALS, WORD PROBLEMS
Focus: CONCEPTUAL UNDERSTANDING & APPLICATION OF SKILLS
Format: Teaching + Worksheets + Discussions
Fee: $90 only.
Tutor: Mr Muhammad Ilyasa (M.Ed., PGDE, B.Sc, Ex-MOE Teacher, Full-Time Tutor of PSLE, ‘O’ and ‘A’ Level Math since 2004).
Mr Ilyasa has been coaching students in Primary, Secondary & JC Math for more than 10 years. An alumnus of RI and RJC, Mr Ilyasa holds both a Master of Education degree and a Postgraduate Diploma in Education with Credit from the National Institute of Education, as well as a Bachelor of Science degree from the National University of Singapore.
TO REGISTER, SMS <STUDENT NAME> , <P4MATHOCT> TO 97860411. Please indicate morning or afternoon.
As places are limited, pre-payment is encouraged to confirm your attendance. You can make cash or cheque payment by visiting the centre at the address above.
P6 MATH (2015) HOLIDAY HEADSTART – SPEED & PROBLEM-SOLVING (starting 6 Dec)
This workshop, over 3 Saturdays, is to introduce current P5 students to a DIFFICULT TOPIC in PSLE MATH – SPEED, and PROBLEM SOLVING involving Speed (this time slot, Sat 9.30 am – 11.15 am, will continue to be the P6 Math weekly tuition slot for 2015)
TO REGISTER, SMS <STUDENT NAME> , <P6MHH> TO 97860411.
Level/Subject: P6 MATH (2015)
Dates: SATURDAYS 6/12, 13/12 and 27/12.
Time: 9.30 am – 11.15 am.
Location: Blk 644, Bukit Batok Central, #01-68. S(650644).
Our location is just a 3-min walk from either the Bukit Batok MRT station or the Bukit Batok Bus Interchange. Buses that stop along the roads surrounding our location are numbers 157, 178, 66, 506, 173, 174, 176, 187, 985. Buses services which terminate at Bukit Batok Bus Interchange are 61, 77, 106, 173, 177, 189, 852, 941, 945, 947.
Focus: Conceptual Understanding
Format: Teaching + Worksheets + Discussions
Fee: Only $120 for all 3 sessions.
Tutor: Mr Ilyasa
Mr Ilyasa has been coaching students in ‘A’ Level & IB Physics and Mathematics for more than 7 years, as well as ‘O’ Level & IP Physics, Additional Math, E. Math and PSLE Math for more than 10 years. An alumnus of RI and RJC, Mr Ilyasa holds both a Master of Education degree and a Postgraduate Diploma in Education with Credit from the National Institute of Education, as well as a Bachelor of Science degree from the National University of Singapore.
TO REGISTER, SMS <STUDENT NAME> , <P6MHH> TO 97860411.
P5 MATH (2015) HOLIDAY HEADSTART – RATIO & PROBLEM-SOLVING (starting 6 Dec)
This workshop, over 3 Saturdays, is to introduce current P4 students to the MOST IMPORTANT TOPIC of PSLE MATH – RATIO, and PROBLEM SOLVING involving Ratios (this time slot, Sat 11.30am – 1.15pm, will continue to be the P5 Math weekly tuition slot for 2015)
TO REGISTER, SMS <STUDENT NAME> , <P5MHH> TO 97860411.
Level/Subject: P5 MATH (2015)
Dates: SATURDAYS 6/12, 13/12 and 27/12.
Time: 11.30 am – 1.15 pm.
Location: Blk 644, Bukit Batok Central, #01-68. S(650644).
Our location is just a 3-min walk from either the Bukit Batok MRT station or the Bukit Batok Bus Interchange. Buses that stop along the roads surrounding our location are numbers 157, 178, 66, 506, 173, 174, 176, 187, 985. Buses services which terminate at Bukit Batok Bus Interchange are 61, 77, 106, 173, 177, 189, 852, 941, 945, 947.
Focus: Conceptual Understanding
Format: Teaching + Worksheets + Discussions
Fee: Only $120 for all 3 sessions.
Tutor: Mr Ilyasa
Mr Ilyasa has been coaching students in ‘A’ Level & IB Physics and Mathematics for more than 7 years, as well as ‘O’ Level & IP Physics, Additional Math, E. Math and PSLE Math for more than 10 years. An alumnus of RI and RJC, Mr Ilyasa holds both a Master of Education degree and a Postgraduate Diploma in Education with Credit from the National Institute of Education, as well as a Bachelor of Science degree from the National University of Singapore.
TO REGISTER, SMS <STUDENT NAME> , <P5MHH> TO 97860411.
PSLE MATH INTENSIVE REVISION STAGE 1 (MAR HOLS)
Conducted by our Principal Tutor, Mr Ilyasa (M.Ed, PGDE, B.Sc) who has been successfully coaching students in PSLE Math Problem-Solving & Heuristics since 2005.
Days/Times (Total 3 days, 6 hrs):
Monday 17 Mar, 2pm – 4pm.
Tuesday 18 Mar, 2pm – 4pm.
Wednesday 19 Mar, 2pm – 4pm.
Location: Blk 627, Bukit Batok Central, #07-640. Singapore 650627.
(Our location is just a 3-min walk from either the Bukit Batok MRT station or the Bukit Batok bus interchange. Buses that stop along the road in front of Blk 627 are numbers 157, 178, 66, 506, 173, 174, 176, 187, 941, 947, 985)
Total Fee: $150
To register, SMS <STUDENT NAME><PSLE> to 97860411 or email to ilyasa@conceptlearning.sg
For enquiries, call Mr Ilyasa directly at 97860411.
Topics for today’s PSLE MATH INTENSIVE REVISION (Sep 9 to Sep 12)
The problem sum concepts that I will be covering in today’s PSLE MATH INTENSIVE REVISION (Sep 9 to Sep 12, Mon to Thurs, 2-4pm) are:
(1) Repeated Identity;
(2) Equal Quantities;
(3) External Transfer with one Unchanged Quantity;
(4) Internal Transfer with Total Quantity Unchanged.
The problem sums will also cover Fractions, Ratios and Percentages.
Rgds,
Ilyasa
Final PSLE Math Intensive Revision (Sep 9 to Sep 12)
For our latest timetable, click here => 
===============================================================
ORIGINAL POST(OUTDATED):
Ok, a parent has asked me abt PSLE Math intensive revision during the Sep hols. Due to my busy schedule, I can only conduct it from 2pm to 4pm, Mon (Sep 9) to Thurs (Sep 12) at Bukit Batok Central Blk 627, near West Mall and Bukit Batok MRT station. Since it is only 8 hrs, I will only cover the heuristics used to solve difficult problem sums, as a last-minute revision of such concepts.
Each 2 hr session is $30. So total fees for four days is $120. Due to limited places (max eight students), confirmation of registration is by advance payment. To register, send an sms to my hp no: 97860411.
This course is personally taught by me, with a focus on thinking skills and metacognition. Please share this post with people who may be interested. Thank you!
Rgds,
Ilyasa,
Principal Tutor, Singapore Learner, Ex-sch teacher, M.Ed, PGDE, B.Sc.
You can view my resume at https://singaporelearner.com/
P5 Challenging Math Weekly Programme
For our latest timetable, click here => 
===============================================================
ORIGINAL POST(OUTDATED):
To register, kindy sms to or call 94468012 or 97860411.
Level/Subject: Primary 5 Challenging Math
Day/Time:
(1) Every Thursday, 4.00 pm to 5.30 pm, OR
(2) Every Saturday, 7.00 pm to 8.30 pm
Location: Blk 627 Bukit Batok Central #07-640
Focus: Difficult Concepts, Strategies, Heuristics, Olympiad
Fees: $120 for every four sessions.
Class Size: 3 to 8 students.
Tutors:
Mr Jay Lim. A Master degree holder, Mr Lim is a very effective and experienced senior tutor who has been tutoring students in PSLE Math & Science for more than 5 years, both in private and in successful learning centres.
Mdm Anu. A Bachelor of Science degree (with Distinction) holder, Mdm Anu is a very caring and passionate tutor who is experienced in coaching P1 to P6 students.
To register, kindy sms to or call 94468012 or 97860411.
P6 MATH & SCIENCE, June INTENSIVE REVISION For PSLE 2013
For our latest timetable, click here => 
===============================================================
ORIGINAL POST(OUTDATED):
For enquires, pls call 97860411, or visit www.conceptlearning.sg
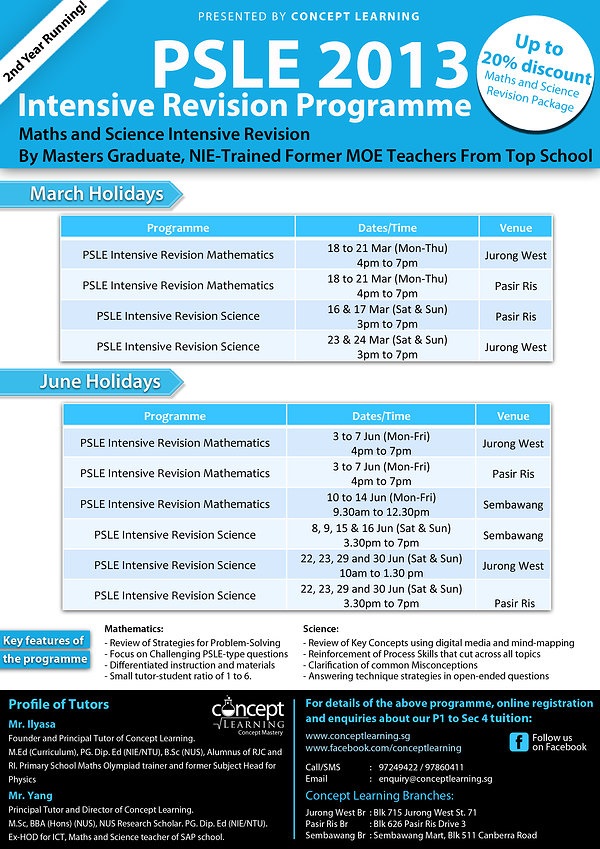
To register for classes at Concept Learning, click here.
The PSLE Intensive Revision in Mathematics is a 4/5-day intensive revision programme conducted during the upcoming March and June school holidays to prepare P6 pupils for the 2013 PSLE Mathematics Examination.
The objectives of the programme are as follows:
- Review of problem-solving strategies to conquer Challenging PSLE maths problems using the Conceptual Approach such as Advance Model Drawing, Remainder Concept (Branching), Repeated Identity, Equal Concept, Unchanged Total, Proportions Concept and Constant Difference. The strategies cuts across the major topics in PSLE such as fractions, ratio, percentage, decimals, measurement and numbers.
- Review and the reinforcement of key topics such as Percentage, Ratio, Fractions, Decimals, Algebra, Geometry, Area and Perimeter and Volume.
A former MOE school teacher, Mr Ilyasa has been coaching students in ‘A’ Level (H2/H1) Physics and (H2/H1) Mathematics for more than 7 years, as well as ‘O’ Level Physics, Additional Math, Math and PSLE Math for more than 10 years. An alumnus of RI and RJC, Mr Ilyasa holds a Bachelor of Science degree with Merit from the National University of Singapore, a Postgraduate Diploma in Education with Credit from the National Institute of Education, Singapore, and a Master of Education (Curriculum & Teaching) degree also from the NIE, Singapore.
An important PSLE math concept to understand (Part 1)
Let me share with you a difficult concept normally tested in P5 or P6 Math. I’m not sure if it has a name. It makes use of the concept of difference between two values but it’s not the same as the Constant Difference concept, which refers to the idea of a particular difference between two values being the same despite making changes to other quantities. The concept that I’m about to introduce actually makes use of TWO differences, the difference between individual values and the difference in their total values. Quite a number of tough P6 qns are actually testing whether students know that there is a relationship between the difference between two individual values and the difference in their total values.
I think this is best explained without any unknown values. Let’s say a pencil costs $1 and a pen costs $1.50. The difference in their values is $0.50 right? Let’s call this the Individual Difference. Let’s say you purchase 10 of each, costing a total of $10 and $15 respectively. The difference in their total values is $5 right? Let’s call this the Total Difference. Is there a relationship between the Individual Difference (ID) and the Total Difference (TD)? Yes. Notice that if TD is divided by ID (5 / 0.50), what you’ll get is 10, which is the number of each item you purchased. If this is easy for you to understand, it is likely because all values are known and you were working forwards to find the total difference, and not working backwards to find the number of each item bought.
Let me now show you how a typical P6 question looks like:
John bought an equal number of pens and pencils. Each pencil costs 50 cents less than a pen. John paid a total of $5 more for the pens than for the pencils. How many pencils did John buy? (using TD/ID, the answer is 10. but notice how intriguing the question has become?)
Please also realise that the concepts of ratio, decimals, fractions and percentages are all related and interchangeable. So let’s make the above question harder:
John bought some pens and pencils. The ratio of the number of pencils he bought to the number of pens is 1:1. Each pencil costs $1 and each pen costs 50% more than a pencil. John paid a total of $5 less for the pencils than for the pens. What is the total number of pens and pencils that John bought? (answer: 20)
Another way of looking at the above problem is to see that since each pencil costs 50 cents less than each pen, it must have taken 10 of them to be a total of $5 less than the SAME quantity of pens.
Rgds,
Ilyasa,
Founder, Singapore Learner; Director, Concept Learning Pte Ltd
Related links:
(1) Challenging PSLE Math Programme for Medium to High Ability Students
(2) P6 MATH & SCIENCE, March & June INTENSIVE REVISION For PSLE 2013
===============================================================
For our latest timetable, click here => 
Reflections on PSLE Math Intensive Revision recently held at Concept Learning
I’ve been wanting to write abt this for some time. For the four days of the PSLE Math Intensive Revision we covered topics such as Remainder Concept, Constant Difference Concept, Internal Transfer Concept and so on, with each worksheet having questions of increasing difficulty involving whole numbers, decimals, fractions, ratios and percentages. For most of the questions, I showed more than one method of solving them, for eg., by using model drawings, units, or the branch method and so on.
So what did I discover from conducting the course? I’m surprised to learn from the students that schools do not cover all the methods I demonstrated, maybe due to a lack of time. And the students, who were abt medium to high ability in math, could solve difficult questions if the question involves only one concept or one method. If the question involves fractions, ratios, decimals and percentages all at the same time, or the question is best done using the branch method first followed by models drawing, then many of the students could not completely solve the problem.
How to overcome the above problem? Students need to understand that fractions, ratios, decimals and percentages all just different forms of the same proportion of quantities, and are thus easily convertible from one form to the other. But students must first understand each concept properly first; for example, what does it mean if the problem has the phrase “John has 25% percent more marbles than Alvin”? If a student is comfortable with using the ratio method to solve problems, but is unable to rewrite the above phrase in ratio form, then he may not be able to proceed with solving the rest of the problem.
Some questions involve more than one concept. For example, it contains a phrase such as “Alvin sold some marbles and gave 40% of the remainder to Susan and Eugene, with Susan getting 20 more marbles than Eugene.” A well-trained student would be able to use a number of methods to solve a difficult problem.
I’m also surprised that some students do not know how to check whether their answers are correct. Since most tough questions require students to work backwards to find some unknown starting quantity, then the student can verify the correctness of his answer by working “forward” with the now known starting quantity and try to obtain all the other quantities given in the question.
The key to solving PSLE math problems is to understand that either a quantity has remained unchanged, or is equal to another, or can be made equal to another. Then the different methods (models, units, branch etc) can be applied.
A very bright student once said to me – “Whether you draw models or use units or use algebra is not important. You must first understand the nature of the problem.”
Good luck.
Ilyasa.
Mr Ilyasa is the Principal Tutor at Concept Learning and Singapore Learner. He can be contacted at 97860411, or ilyasa@conceptlearning.sg.
* If you are medium or high ability student preparing for PSLE Math, you may want to attend my weekly workshop: Challenging PSLE Math Programme for Medium to High Ability Students. In this programme, I will also include P6 Math Olympiad problems that are relevant to the PSLE.
_______________________________________
TUITION CLASSES:
_______________________________________________________________
EDUCATIONAL SERVICES:
______________________________________________________________







